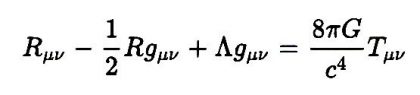奥州宇宙遊学館

―　一般相対性理論より　―

1915年に発表された一般相対性理論の骨子である「アインシュタイン方程式」の特殊解として、ブラック
ホールの存在が予測されました。

・・・・・・（1）

（1）式は、重力場方程式と呼ばれるもので、「物質があると時空はどう曲がるのか」を示す式です。左辺は
「時空のゆがみ具合」を示し、右辺は「物質が持つエネルギー」を示します。この式を解くと、星や銀河などの
物質の重力により宇宙は収縮して終わりを迎えることになります。そこでアインシュタインは、重力を押し返す
力（斥力）を持たせるために宇宙定数と呼ばれる「Λｇ_μｖ」を書き加えます。

・・・・・・(2)

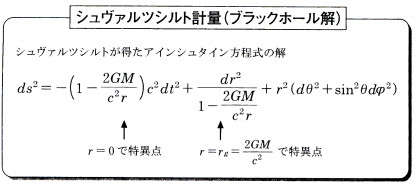
この（2）式について、ドイツ・ポツダム天文台長のカール・シュヴァルツシルトが、「球状の天体があり、
その周辺が真空」という仮定条件のもと、「時空（時間と空間）が球対称」という条件を付けて方程式を
解きました。すなわち、「時空が真空で（アインシュタイン方程式の右辺がゼロ）、中心にだけに星がある
ような球対称構造で、さらに時間変化しない場合」という条件です。

ここで、Mは質量。Gは万有引力定数、cは光速を表わし、rは球対称時空の動径半径を表わします。

シュヴァルツシルトの解には、不思議な点が含まれています。「無限大」が発生する箇所が2つあります。
1つはr＝0で、中心点の時空特異点（物質を置いたところの原点）です。もう一つはr＝r_gです。これは
「シュヴァルツシルト半径」と呼ばれます。r＝0の特異点がブラックホールの中心であり、r＝r_gの特異点が
ブラックホールの「地平面の位置」を表わします。すなわち、この地平面は強い重力の影響で光さえも脱出
できないブラックホールの「境界面」を表わしているのです。

この「シュヴァルツシルト半径」はどのような物体に対しても計算することができます。例えば質量が
1.989×10²⁷kg、大きさが6.96×10⁵kmの太陽のシュヴァルツシルト半径は、約3kmとなります。すなわち、
太陽がそのままの質量で、その大きさを約3kmにまでギューッと圧縮したとするとブラックホールにります。
同様に地球の場合（質量5.972×10²⁴kg、大きさ6365km）のシュヴァルツシルト半径は、約9mmとなります。

このように天体の質量とサイズとから、その天体がブラックホールであるかどうか推測することができます。

―　強力X線源による判定　―

ブラックホールを見い出す手がかりの一つとして、強力なX線を発生している天体があります。しかし
ちょっと不思議なことですが、光と同じ電磁波であるX線を発生している天体が、ブラックホールだなんて？

ブラックホールからのX線発生のメカニズムは、「なぜ光と同じ電磁波であるX線がブラックホールから
出られるのか？」の項で説明したように、ブラックホールはペアである恒星のガスをはぎ取ることができ、
はぎ取られたガスがブラックホール周辺に「降着円盤」を形成し、その円盤の中心が1000万度近くにまでなり、
X線が発生・放射される、と考えられているからです。この時このX線は、強い重力で赤方偏移（スペクトルが
長波長側（可視光でいうと赤に近い方にずれる））により、より短い波長の電磁波になり、強いX線（源）に
なります。これだけのエネルギーを放出することができるような仕組みは、ブラックホール以外に考えらえない
ということで、現在は強いX線源は、ブラックホールと考えられています。